Baza dimensiune a spațiului vectorial și

Când am discutat conceptul de vector n-dimensional și introdus în funcțiune pe vectori, am aflat că mulțimea tuturor vectorilor n-dimensionale generează un spațiu liniar. În acest articol vom vorbi despre cele mai importante concepte legate - pe dimensiunea și o bază a spațiului vectorial. De asemenea, luați în considerare teoria descompunerii unui vector arbitrar în baza și relația dintre diferitele baze de spațiu n-dimensional. Noi analizăm în detaliu exemple specifice de soluții.

Navigare în pagină.

Conceptul unui spațiu vectorial de dimensiune și de bază.

Dimensiunea unui spațiu vectorial este numărul egal cu numărul maxim de vectori liniar independenți în acest spațiu.

Bazele spațiului vectorial - un set ordonat de vectori liniar independenți în acest spațiu, numărul de care este egală cu dimensiunea spațiului.

Iată câteva considerații pe baza acestor definiții.

Luați în considerare spațiul vectorilor n-dimensionale.

Arătăm că dimensiunea acestui spațiu este egală cu n.

Să luăm un sistem de vectori n unități ale formei

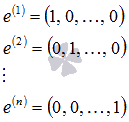
Să presupunem ca acești vectori rânduri ale matricei A. În acest caz, matricea A este o matrice unitate de dimensiune n la n. Rangul acestei matrice este egal cu n (dacă este necesar, a se vedea articolul rang matrice: determinarea, găsirea tehnici). Prin urmare, sistemul de vectori este liniar independent, iar acest sistem nu se poate adăuga un singur vector fără a încălca independența liniară. Deoarece numărul de vectori din sistem egal cu n. dimensiunea spațiului vectorilor n-dimensionale egal cu n. și vectori de unitate formează o bază a acestui spațiu.

Ultima aserțiune și determinarea bazei, putem concluziona că orice sistem de vectori n-dimensionale, numărul de vectori în care mai puțin de n. Nu este o bază.

Acum, schimba primul și al doilea sistem de vector. Este ușor de a arăta că sistemul de vector rezultat este, de asemenea, o bază de spațiu vectorial n-dimensional. Compoziția matricei, luând vectorilor rând acestui sistem. Această matrice poate fi derivată din matricea de identitate prin schimbul prima și a doua linii, prin urmare, rangul său este egal cu n. Astfel, sistemul de n vectori liniar independenți și un spațiu vectorial bază n -dimensional.

Dacă schimb ceilalți vectori ai sistemului, vom găsi o altă bază.

Dacă luați un sistem liniar independent nu este vectori unitate, este, de asemenea, baza de spațiu vectorial n-dimensional.

Astfel, spațiul vectorial de dimensiune n are cât mai multe baze ca sunt liniar sistem independent de vectori n-dimensionale n.

Dacă vorbim despre spațiul vectorial bidimensional (adică, pe plan), baza sa sunt oricare doi vectori non-coliniare. Baza de spațiu tridimensional sunt orice trei vectori non-coplanare.

Luați în considerare câteva exemple.

Sunt vectorii de baza spațiului vectorial tridimensional?

Vectorii de descompunere în spațiul vectorial bază.

Să vectori sunt arbitrare baza spațiului vectorial n-dimensional. Dacă adăugăm la aceasta un vector x n-dimensional. sistemul rezultat al vectorilor este dependentă liniar. știm că cel puțin un vector este liniar sistem dependent este exprimat în termeni de celălalt liniar dintr-o dependență liniară a proprietăților. Cu alte cuvinte, cel puțin unul dintre vectorii sunt sistem liniar dependente împarte vectorii rămași.

Aceasta ne aduce la o teoremă foarte importantă.

Orice vector n spațiu vectorial -dimensional descompus în mod unic în baza.

Să - baza de spațiu vectorial n-dimensional. Noi adăugăm la acești vectori n-dimensional vector x. Apoi, sistemul rezultat al vectorilor este liniar dependent și vectorul x poate fi exprimată liniar în termeni de vectori, în cazul în care - unele numere. Așa că am obținut o extindere a lui x în baza. Rămâne să dovedească faptul că această descompunere este unic.

Să presupunem că există o altă descompunere, în cazul în care - unele numere. Scădeți din stânga și din dreapta părțile laterale ale ultima egalitate, respectiv, partea stângă și dreaptă a ecuației:

Deoarece sistemul de vectori de bază este liniar independentă, atunci prin definiție independența liniară a vectorilor care rezultă egalitatea este posibilă numai dacă toți coeficienții egali cu zero. Prin urmare, ceea ce se dovedește vectorul de descompunere unicitatea în baza.

Coeficienții se numesc coordonatele x in baza.

După ce a devenit familiarizat cu teorema privind descompunerea vectorului în baza, vom începe să înțelegem esența expresiei „ni se dă un vector n-dimensional.“ Această expresie înseamnă că considerăm spațiul vectorial n-dimensional vector x, ale cărei coordonate sunt date într-un anumit mod. În același timp, ne dăm seama că același vector x la o altă bază de spațiu vectorial n-dimensional va avea coordonatele care sunt diferite de.

Luați în considerare următoarea problemă.

Să presupunem că în unele baze de spațiu vectorial n-dimensional ni se un sistem de vectori liniar independenți n

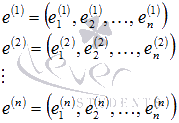
și un vector. Apoi vectorii sunt, de asemenea, în baza acestui spațiu vectorial.

Să presupunem că vrem să găsim coordonatele vectorului x în baza. Notăm aceste coordonate, cum ar fi.

Vectorului x în baza unei reprezentări. Scriem această ecuație în forma de coordonate:

Această ecuație este echivalentă cu un sistem de n ecuații liniare cu n variabile necunoscute:

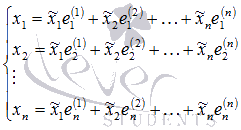
Rezumatul sistemului de matrice are forma

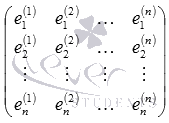
Vom nota prin litera A. Coloanele A sunt liniar vectori independenți de vectori, astfel încât gradul de această matrice este egal cu n. Prin urmare, determinantul său este nenul. Acest fapt indică faptul că sistemul are o soluție unică, care poate fi găsit prin orice metodă, de exemplu, prin Kramer sau metoda de matrice.

Deoarece coordonatele dorite ale lui x în baza va fi găsit.

Să examinăm teoria cu exemple.

Într-o bază a unui spațiu vectorial tridimensional dat vectori

Asigurați-vă că sistemul de vectori este, de asemenea, o bază a acestui spațiu și de a găsi coordonatele vectorului x în această bază.

Sistemul vectorial a stat la baza spațiului vectorial tridimensional este necesar, astfel încât este liniar independentă. Să explicăm acest lucru prin definirea rangul de A. rânduri sunt vectori. Locul găsit metoda Gauss

De aceea, Rank (A) = 3. arată că independența vectorilor lineare.

Deci, sunt vectorii de bază. Lăsați această bază vector x are coordonatele. Apoi, așa cum am arătat mai sus, relația este definită de coordonatele sistemului vector de ecuații

Substituind cunoscut din valorile de condiție, obținem

Noi rezolva de Kramer:

Astfel, vectorul x are o bază coordonate.

.