Cum de a găsi mărimea vectorului

anterior ◈ următoarea

Vector - un obiect geometric care se caracterizează prin atât magnitudinea și direcția. [1] Mărimea unui vector este lungimea sa, și corespunde direcției la care. Mărimea vectorului este calculată destul de ușor, pentru ca aceasta să facă câțiva pași simpli. Alte operații importante cu vectori includ adunarea și scăderea vectorilor, găsind unghiul dintre cei doi vectori și calcularea produsului vectorial.







pași Editare

Metoda 1 de la 2:
Calcularea vectorului care vine de la origine Editare

Cum de a găsi mărimea vectorului

Cum de a găsi mărimea vectorului

Definiți componentele vectorului. Orice vector pe planul poate fi reprezentat numeric într-un sistem de coordonate cartezian bidimensional cu două numere: orizontală (axa X) și componenta verticală (axa Y). [2] Vectorul poate fi scris ca o pereche de numere: v = .
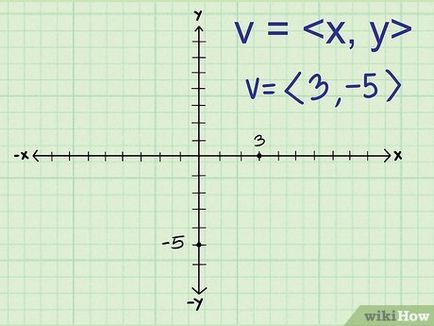
  • De exemplu, în cazul în care componenta orizontală a vectorului este egal cu 3, iar pe verticală este de -5, acest vector este scris ca <3, -5>.

Cum de a găsi mărimea vectorului

Cum de a găsi mărimea vectorului

Desena un triunghi vector. Dacă ați pus componentele orizontale și verticale, veți avea un triunghi dreptunghic. Amploarea vectorului este lungimea ipotenuzei triunghiului, și pentru calculul acestuia, puteți utiliza teorema lui Pitagora.

Cum de a găsi mărimea vectorului

Cum de a găsi mărimea vectorului

Pentru a calcula vectorii, înregistrați teorema lui Pitagora. Teorema lui Pitagora afirmă că suma pătratelor picioarele unui triunghi dreptunghic este egal cu pătratul ipotenuzei sale: A 2 + B 2 = C 2. în acest caz, „A“ și „B“ - este componentele vectoriale orizontale și verticale, și „C“ reprezintă ipotenuza. Deoarece ipotenuzei este doar un vector, este necesar să se găsească o „C“.





  • x 2 + y 2 = v 2
  • v = √ (x 2 + y 2))

Cum de a găsi mărimea vectorului

Cum de a găsi mărimea vectorului

Găsiți magnitudinea vectorului. Pentru acest substitut într-o ecuație valorile numerice obținute mai sus, adică componentele vectorului respectiv.
  • În acest exemplu v = √ ((martie-2 + (- 5) 2))
  • v = √ (25 + 9) = √34 = 5831
  • Nu vă lăsați înșelați dacă rezultatul nu a fost un număr întreg. Lungimea vectorului poate fi o valoare fracțională.

Metoda 2 din 2:
Găsirea valoarea vectorului, începutul care nu coincide cu originea Editare

Cum de a găsi mărimea vectorului

Cum de a găsi mărimea vectorului

Se determină coordonatele începutul și sfârșitul vectorului. Orice vector pe planul poate fi reprezentat numeric într-un sistem de coordonate cartezian bidimensional cu două numere: orizontală (axa X) și componenta verticală (axa Y). [3] Vectorul poate fi scris ca o pereche de numere: v = . Dacă începutul vectorului nu coincide cu începutul unui sistem de coordonate cartezian, este necesar să se determine coordonatele vectorului punct de început și de sfârșit.
  • Lăsați vectorul AB conectarea punctelor A și B.
  • Un punct de a coordona orizontală și verticală de coordonate de 5 1, astfel încât coordonatele pot fi exprimate ca perechi de numere <5, 1>.
  • Punctul B are coordonate orizontale și verticale de coordonate 1 2, prin urmare coordonatele sale pot fi exprimate ca perechi de numere <1, 2>.

Cum de a găsi mărimea vectorului

Cum de a găsi mărimea vectorului

Pentru a găsi mărimea vectorului, folosind o formulă modificată. Deoarece, în acest caz, având în vedere coordonatele a două puncte trebuie scăzute coordonatele x și y de un punct de coordonatele corespunzătoare ale doilea punct: v = √ ((x2 -X1) 2 + (y2 -Y1) 2). [4]
  • Să punctul A are coordonatele , și punctul B - coordonatele

Cum de a găsi mărimea vectorului

Cum de a găsi mărimea vectorului

Găsiți magnitudinea vectorului. Puneți coordonatele punctelor în ecuație și se calculează lungimea vectorului. În acest exemplu, calculul este după cum urmează:
  • v = √ ((-X1 x2) 2 + (y2 -Y1) 2)
  • v = √ ((1-5) 2 + (2-1) 2)
  • v = √ ((- 4) 2 + (1) 2)
  • v = √ (16 + 1) = √ (17) = 4,12
  • Nu vă lăsați înșelați dacă rezultatul nu a fost un număr întreg. Lungimea vectorului poate fi o valoare fracțională.






anterior ◈ următoarea