densitate de probabilitate
Continuă cu. în. Puteți specifica o funcție, care se numește distribuția densității sau a densității de probabilitate, sau funcția de distribuție diferențială.
Funcția densitate de probabilitate cu continuă. în. X se numește funcția f (x) - prima derivată a funcției de distribuție F (x):
Din această definiție, rezultă că funcția de distribuție este primitiv pentru distribuția densității.
Pentru a descrie distribuția de probabilitate discrete cu. în. densitatea de distribuție nu se aplică.
Sensul probabilistic al distribuției densității.
Astfel, limita raportului dintre probabilitatea ca un p continuu. în. presupune valoarea aparținând intervalului (x, x + Ax), lungimea acestui interval (→ 0 când Ax) este egală cu valoarea distribuției densității la punctul x.
Funcția de densitate caracterizează fiecare valoare variabilă aleatoare continuă în mod individual, mai degrabă decât o gamă așa cum este cazul pentru funcția de distribuție.
Șansa de a lovi cu continuu. în. la un interval predeterminat.
Potrivit Newton - Leibniz:
Găsirea funcției de distribuție a unei funcții de densitate cunoscută.
Punerea anterioară formula a = -∞, b = x, și înlocuirea variabilei de integrare x cu t, avem:

Proprietățile de densitate de probabilitate
Proprietatea 1. Densitatea de distribuție - funcția negativă: f (x) 0 (ca funcția cumulativă de distribuție - funcția non-descreștere, iar densitatea de distribuție a primului derivat).
Dovada. integrală improprie
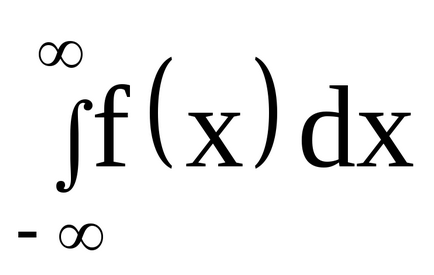
Geometric, acest lucru înseamnă că întreaga suprafață a trapezului curbiliniu delimitat de 0x axa și curba de distribuție este egal cu unu.
Vchastnosti dacă toate valorile posibile ale variabilei aleatoare aparțin intervalului (a, b),

distribuție posibilă densitate cronologică (exemplu)
f1 (x) - densitatea sumei câștigătoare în primul joc
f2 (x) - densitatea sumei câștigătoare în al doilea joc
Ce joc este de preferat?
Caracteristici numerice ale variabilelor aleatoare.
Aceste caracteristici fac posibilă pentru a rezolva multe probleme fără a cunoaște legea distribuției variabilelor aleatoare.
Caracteristicile poziției variabile aleatoare pe axa reală.
Așteptarea aceasta este valoarea medie ponderată a variabila aleatoare X, în care abscisa fiecărui punct xi este inclus cu „greutate“ egală cu probabilitățile respective.
Așteptarea matematică este uneori menționată pur și simplu ca valoarea medie a rv
Pentru o variabilă aleatoare discretă
Pentru variabila aleatoare continuă
Moda - este valoarea cea mai probabilă a variabilei aleatoare (adică pentru care distribuția densității de probabilitate sau pi f (x) atinge valoarea maximă.).
Distinge de distribuție unimodală (au un mod), distribuție multimodală (au mai multe moduri) și animodalnye (nu de moda)