Dependența liniară a vectorilor
Determinarea independenței liniare a vectorilor
A1 sistem de vectori. A2. Un numit liniar independent. în cazul în care o combinație liniară a acestor vectori λ1 * A1 + λ2 * A2 +. + Λn * Un egal cu vectorul zero, doar la setul zero al numerelor λ1, λ2. λn. adică, sistemul de ecuații: A1 x1 + x2 + A2. + O xn = θ are doar soluția banală.
Verificați dacă sistemul este vectori liniar dependent
1. Asigurați-un sistem de ecuații:
2. Rezolvați de Gauss. Sistemul de conversie Iordania sunt enumerate în Tabelul 29.1. La calcularea laturile din dreapta ale sistemului nu sunt înregistrate, deoarece acestea sunt zero și Iordania nu sunt modificate în conversie.
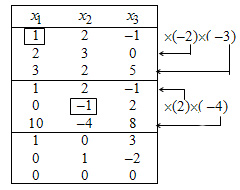
3. Din ultimele trei rânduri din tabel scrie sistemul de permise, care este echivalent cu sistemul original:
4. Ia soluția generală:
5. Definiți la valoarea sa discreție a x3 variabila liberă = 1, obținem soluția nontrivial privată X = (- 3,2,1).
A: Astfel, pentru non-zero, set de numere (-3,2,1) combinația liniară a vectorilor este egal cu zero vector -3A1 + 2A2 + 1A3 = θ. Prin urmare, sistemul de vectori este liniar dependent.
Proprietățile sistemelor vectoriale
Proprietate (1)
În cazul în care sistemul de vectori este liniar dependent, atunci cel puțin unul dintre vectorii extinse în altele și, dimpotrivă, în cazul în care cel puțin unul dintre vectorii sistemului poate fi extins pentru restul, sistemul de vectori este liniar dependent.
Proprietate (2)
În cazul în care orice vectori subsistem sunt liniar dependente, atunci întregul sistem este dependentă liniar.
Proprietate (3)
Dacă sistemul este liniar vectori independenți, atunci orice subsistem este liniar independent.
Proprietate (4)
Orice sistem de vectori conținând vectorul zero, este dependentă liniar.
Proprietatea (5)
Sistemul vectorilor m-dimensionale este întotdeauna dependentă liniar dacă n este mai mare decât numărul de vectori de dimensiune (n> m)
sistem vector Basis
r - numărul vectorilor incluși în baza.
Teorema 29.1 Despre sistemul de vectori de bază unitate.
Dacă sistemul este vectori m-dimensionale care cuprinde m unitate diferiți vectori E1 E2. Em. ele formează baza sistemului.
Algoritmul pentru identificarea vectorilor de bază de sistem
În scopul de a găsi o bază de vectori A1, A2. Un necesar:
- Crearea unui sistem vector adecvat de omogen ecuații A1 x1 + A2 x2 +. + O xn = θ
- Adu acest sistem
