Exemple de soluții de serie, matematici superioare
Exemplu. Un studiu privind convergența și suma seriei.
Având în vedere: un număr
Găsiți: suma seriei în cazul convergenței.
Noi reprezentăm un număr de membri ca suma a doi termeni:
Se pare că suma parțială n-lea al seriei poate fi scrisă ca:
Rezultă că.
Seria converge. un număr egal cu suma.
Exemplu. Un criteriu necesar de convergență a seriei.
Având în vedere: un număr
Caută:
Verificați dacă semnul necesar de convergență a seriei.
atribut necesar de convergență a seriei constă în faptul că, în cazul în care seria numerică converge,
În consecință, în cazul în care un ≠ 0, atunci seria este divergenta.
Pentru o anumită sarcină într-o serie de numere:
≠ 0. Mai multe divergente.
Exemple. Suficientă pentru convergența seriilor pozitive.
Având în vedere: ranguri
1)
2)
3)
4)
5)

6)
Caută:
Exploreaza convergența seriei.
1) Pe baza faptului că, în toate ≤ n și converge seriile armonice generalizate, rezultă că un număr mai mic de membri convergente.
2) Pe baza faptului că, în cazul în care condițiile sunt îndeplinite: ln n ≥ 0 pentru n ≥ 1, apoi la ≥ n ≥ 1.
Seria armonică generalizată divergenta, prin urmare, un număr de membri mari diverge.
3) De la un număr de separat partea principală a nth membru: ca n → ∞ ∼ .
Un număr predeterminat și un număr de același comportament ca și.
Seria geometrică converge, apoi seria de asemenea converge.
4) selectați dintr-un număr de partea principală a nth membru: ca n → ∞ ∼ .
comandă <1, поэтому ряд расходится.
5) dintr-un număr de
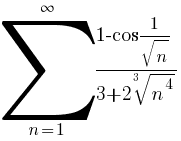
când n → ∞ ∼ .
Ordinea> 1, astfel încât seria converge.
6) Din seria evidenția partea principală a n termen al seriei-lea:
când n → ∞ ∼
Procedura, prin urmare, seria diverge.