Funcția de putere - studopediya
Funcția unde x - variabila, un - un anumit număr, numit o funcție de putere.
Dacă ceva - o funcție liniară, graficul acesteia - o linie dreaptă (vezi secțiunea 4.3, figura 4.7 ..).
Dacă ceva - o funcție pătratică, graficul acesteia - un parabole (vezi pct 4.3, figura 4.8 ..).
Dacă graficul său - parabolei cubic (vezi secțiunea 4.3, figura 4.9 ..).
Aceasta este funcția inversă a
1. Definiții Field:
2. Setul de valori:
3. Paritatea ciudat: funcția de ciudat.
4. Frecvența funcțiilor: non-periodice.
5. zerourilor: x = 0 - un singur zero.
6. Valorile maxime și minime ale funcției: cele mai mari și cele mai mici valori ale funcției nu are.
7. Intervalele de creștere și descreștere: funcția este în creștere pe domeniul său.
8. Graful parabolei cubice grafice simetrice respectă pe linia y = x și este reprezentată în Fig. 5.1.
1. Definiții Field:
2. Setul de valori:
3. Paritatea ciudat: funcția este chiar.
4. Frecvența funcțiilor: non-periodice.
5. zerourilor: unic zero, x = 0.
6. Valorile maxime și minime ale funcției: ia cea mai mică valoare pentru x = 0 și este egal cu 0.
7. Intervalele de creștere și descreștere: funcția este în scădere pe intervalul și creșterea diferenței
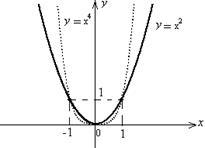
8. Funcția Program (pentru fiecare n Î N) «similar» pe graficul unei parabole pătratice (graficele funcțiilor sunt prezentate în Fig. 5.2).
1. Definiții Field:
2. Setul de valori:
3. Paritatea ciudat: funcția de ciudat.
4. Frecvența funcțiilor: non-periodice.
5. zerourile funcției: x = 0 -uniqueness zero.
6. Valorile maxime și minime sunt valori maxime și minime a funcției nu în nici
7. Intervalele de creștere și descreștere: funcția este în creștere pe domeniul său.
8. Funcția Program (pentru fiecare), „similar“ graficul parabolei cubice (funcții grafice prezentate în Fig. 5.3).
1. Definiții Field:
2. Setul de valori:
3. Paritate și Odd: Funcția nu are proprietatea de paritate și impar.
4. Frecvența funcțiilor: non-periodice.
5. zerourile funcției: x = 0 -uniqueness zero.
6. maximă și valorile minime ale funcției: Cea mai mică valoare de 0, funcția ia punctul x = 0; cele mai irelevante.
7. Intervalele de creștere și descreștere: funcția este în creștere pe domeniul său.
8. Fiecare astfel de funcție într-un anumit indice este inversul funcțiilor furnizate
9. Graph „like“ funcția pe graficul funcției pentru orice n și este prezentată în Fig. 5.6.
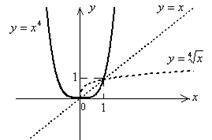
1. Definiții Field:
2. Setul de valori:
3. Paritatea ciudat: funcția de ciudat.
4. Frecvența funcțiilor: non-periodice.
5. zerourilor: x = 0 - un singur zero.
6. Valorile maxime și minime ale funcției: cele mai mari și cele mai mici valori ale funcției nu în nici
7. Intervalele de creștere și descreștere: funcția este în creștere pe domeniul său.
8. Graficul funcției prezentate în Fig. 5.7.
Exemplul 1. Plot caracteristici:
Decizie. 1) Pentru a reprezenta grafic această funcție folosind un grafic reguli de transformare:
a) construirea unui grafic funcție (prezentată în figura 5.7) .;
b) obținem graficul funcției graficului prin transfer paralel-l la o unitate la dreapta de-a lungul axei x și două unități în jos de-a lungul axei y;
c) graficul funcției inițiale se obține din graficul părții de rezervă a graficului spre dreapta axa y și axa y. Altele - aruncare înapoi (Figura 5.8 este prezentat prin liniile punctate.). Porțiunea rămasă a graficului complement simetric l în raport cu axa y (fig. 5.8).
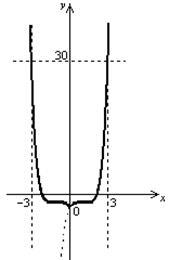
2) Transformarea funcției în formă nota că graficul acestei funcții se obține prin următoarele transformări:
a) construi un grafic al funcției
b) Graficul este obținut din maparea anterioară simetrică în raport cu axa Oy;
c) se obține graficul funcției precedente contrabalansată de 4 unități la dreapta de-a lungul axei x;
g) un grafic funcție predeterminată este obținută din graficul unei deplasare paralelă a două unități sale în jos de-a lungul axei y (fig. 5.9).