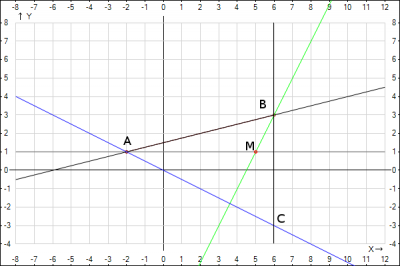
Găsiți ecuația de laturile triunghiului seekland studenți Informații despre comunitate Mutual și elevi

1. Ecuația liniei AB
Două vârfuri sunt, de exemplu, o parte a ecuației poate fi obținută ca o ecuație a unei linii drepte care trece prin cele două puncte având în vedere # 92 $$; Frac = # 92; Frac $$ Substitut A coordonatele nodurilor (-2.1) V (6, 3) în ecuație și obține $$ # 92; = # 92 frac; Frac => y = # 92; fracx + # 92; Frac $$

Pentru a găsi ecuația laturilor rămase,
Noi găsim ecuația de înălțime:
2. A trece prin vârful și perpendicular pe BC, numesc AM. Două puncte au cunoscut, se aplică o ecuație liniară care trece prin cele două punctele A (-2,1), M (5, 1) # 92 $$; Frac = # 92; Frac $$ Tk. y la numitor avem 0, atunci o paralelă directă cu axa Ox și ecuația acesteia # 92; (y = 1 # 92;)
3. B care trece prin vârful și perpendicular pe AC, este numit BM. Două puncte au cunoscut, se aplică o ecuație liniară care trece prin două puncte date B (6, 3), M (5, 1) # 92 $$; Frac = # 92; = Frac> y = 2x-9 $$

Ecuațiile acestor înălțimi, am fost doar în căutarea pentru un singur lucru: după cum știm pantele liniilor perpendiculare sunt conectate prin relația următoare # 92; (k_1 = - # 92; 92 # Frac;), adică ecuații pentru cele două părți rămase, avem una din partea de sus și pantele. Obținem aceste ecuații:
4. Ecuația liniei de curent alternativ. Pentru această ecuație avem coordonatele nodului A (-2,1) și găsi pantă, cunoscând panta liniei drepte perpendiculare BM, care este egal cu # 92; (k_ = 2 # 92) => # 92; (k_ = - # 92; Frac> = - # 92; 92 # Frac;). Apoi ecuația liniei AC este egal cu y-$$ 1 = - # 92; Frac (x + 2) => y = - # 92; fracx $$
5. Ecuația liniei BC. Este cunoscut faptul că înălțimea AM perpendicular pe această latură paralelă cu axa Ox, atunci această parte este paralelă cu axa Oy, și în acest caz, trec prin vertex B (6, 3), adică ecuația lui este # 92; (x = 6, # 92;)

Ecuațiile trei laturi drepte ale triunghiului se găsesc. stand up triunghi