Legea conservării impulsului, cinetică și energia potențială, puterea forțelor de examen fizicii

impuls al corpului

impuls al corpului este o cantitate egală cu produsul din greutatea corpului la viteza sa.

Trebuie reamintit faptul că acesta este un organism care poate fi reprezentat ca un punct material. impuls al corpului ($ p $) este, de asemenea, numit impuls. Conceptul de impuls a fost introdus în fizică Rene Descartes (1596-1650). Termenul „pulsul“ a apărut mai târziu (impulsus în latină înseamnă „push“). Momentum este o mărime vectorială (și viteză) și exprimată prin formula:

direcția vectorului impuls coincide întotdeauna cu direcția vitezei.

Per unitate de impuls în pulsul SI accepta greutate corporală $ $ 1 kg se deplasează la $ $ 1 m / s, prin urmare, unitatea de impuls este de $ 1 kg $ $ $ · m / s.

În cazul în care corpul (punct material) forța constantă pe o perioadă de timp Ot $ $, atunci constanta va fi accelerată:

în care, $ ↖ $ și $ ↖ $ - viteză inițială și finală a corpului. Substituind această valoare în expresia legii a doua a lui Newton, obținem:

Extinderea parantezele și folosirea expresiei pentru impulsul unui corp, avem:

Aici $ ↖-↖ = Δp↖ $ - schimbare de impuls în timpul Ot $ $. Apoi ecuația precedentă devine:

Expresia $ Δp↖ = $ F↖Δt este o notație matematică a doua lege a lui Newton.

O forță de muncă pe durata de valabilitate a acestuia se numește rezistență impuls. Prin urmare, modificarea punctului de impuls este egală cu impulsul de schimbare care acționează pe ea.

Expression $ Δp↖ = F↖Δt $ numită ecuația de mișcare a corpului. Trebuie remarcat faptul că una și aceeași acțiune - punctul de schimbare a impulsului - poate fi obținut printr-o forță mică într-un interval de timp lung și o forță mare pentru o perioadă mică de timp.

Impulsul unui sistem de corpuri. Legea de schimbare a impulsului

Momentum (cantitatea de mișcare) a sistemului mecanic este un vector egal cu suma impulsuri de puncte importante ale sistemului:

Legile și modificări sunt o consecință a conservării impulsului și a treia lege a lui Newton-al doilea.

Să considerăm un sistem format din două corpuri. Forța ($ F_ $ și $ F_ $ în figură, sistemul de corp cu care interacționează unul cu altul sunt denumiți intern.

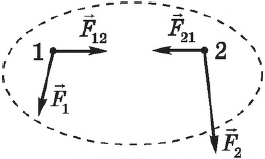
Să presupunem că, în plus față de forțele interne acționează asupra sistemului de forțe externe, și $ $ $ ↖ ↖ $. Pentru fiecare corp se poate scrie ecuația $ Δp↖ = F↖Δt $. Plierea partea stângă și dreaptă ale acestor ecuații, obținem:

Potrivit lui Newton a treia lege $> ↖ = -> ↖ $.

Pe partea stângă este suma geometrică a modificărilor în pulsul tuturor organelor sistemului, care este egală cu o schimbare în impulsul sistemului - $> ↖ $ .Cu acest lucru în minte, egalitatea $ ↖ + ↖ = (↖ + ↖) At $ poate fi scris:

în cazul în care $ F↖ $ - suma tuturor forțelor externe, care acționează asupra organismului. Acest rezultat înseamnă că sistemul de impulsuri poate fi modificat numai impuls schimbare de forțe externe, sistemul este îndreptat precum și forța externă totală. Aceasta este esența legii de schimbare a impulsului unui sistem mecanic.

Forțele interne schimbă impulsul total al sistemului nu se poate. Ei schimba doar impulsurile corpurilor individuale ale sistemului.

Legea conservării impulsului

Din ecuația $> ↖ = $ F↖Δt urmează legea conservării impulsului. În cazul în care sistemul nu este afectat de nicio forță exterioară, partea dreaptă a ecuației $> ↖ = $ F↖Δt dispare, ceea ce înseamnă un impuls totală constantă a sistemului:

Sistemul, pentru care nici o forță externă sau rezultanta forțelor exterioare este nulă, se numește închisă.

Legea conservării stărilor de impuls:

corpuri de impulsuri de sinteză sistem închis rămâne constantă pentru orice interacțiuni între un sistem de corpuri.

Rezultatul este valabil pentru un sistem care conține orice număr de organisme. În cazul în care suma forțelor externe nu este zero, dar suma proiecțiile lor pentru o anumită direcție este zero, sistemul de proiecție a impulsului în această direcție nu se schimba. De exemplu, un sistem de corpuri de pe suprafața Pământului nu poate fi închisă datorită forței de gravitație care acționează asupra întregului corp, dar cantitatea de impulsuri de proiecție pe direcția orizontală poate rămâne neschimbată (în absența de frecare), t. K. Direcția forței gravitației nu este acte.

motor cu reacție

Luați în considerare exemplele care confirmă validitatea legii conservării impulsului.

Ia minge de cauciuc pentru copii, și să meargă din Nadu lui. Vom vedea că, atunci când aerul începe să iasă din ea într-un fel, mingea se va zbura la alta. mișcare Ball este un exemplu de propulsie cu jet. Aceasta se explică prin legea conservării impulsului: totale impuls „minge acesta plus aer“ înainte de expirarea aerului este zero; aceasta ar trebui să rămână la zero în timpul deplasării; însă mingea se mișcă în direcția opusă a descărcării jet, și la o astfel de viteză încât modulo său impulsului egală cu impulsul curentului de aer.

mișcare reactivă se referă la mișcarea corpului care are loc atunci când este separat de acesta cu o viteză a oricărei părți a acesteia. Datorită legii conservării impulsului pe direcția de deplasare a corpului, în timp ce direcția opusă a autoproclamatei.

Pe principiul zborurilor de rachete pe bază de propulsie cu jet. rachetă spațială modernă este un avion foarte complex. racheta în masă este format din fluidul de lucru de masă (m. e. gazele fierbinți rezultate din arderea combustibilului și evacuate ca jet), iar cele din urmă, sau se spune „uscat“ racheta masa rămasă după ejectarea racheta fluidului de lucru.

Când jetul de gaz reactiv cu mare viteză ejectată de racheta, racheta se tinde în direcția opusă. Conform legii conservării impulsului, impulsul $ M_

υ_p $, rachete achiziționate trebuie să fie egal cu puls $ M_ · υ_ $ ejectat gaze:

Acest lucru implică faptul că viteza rachetei

Această formulă arată că cea mai mare viteza rachetei, cu atât mai mare raportul de viteză a gazelor de eșapament și masa fluidului de lucru (m. E. Greutatea combustibilului) la capătul ( „uscat“) greutatea rachetei.

Formula $ υ_p = (> /) · $ υ_ este aproximativă. Nu se consideră că ca masa de ardere care zboară rachete devine mai puțin și mai puțin. Formula exactă pentru viteza rachetei a fost obținută în 1897 K. E. Tsiolkovskim și poartă numele.

Tsiolkovsky formulă ne permite să calculeze rezervele de combustibil necesare pentru posturile specificate de rachete de viteză.

forță de muncă

Termenul „lucrarea“ a fost introdus în fizică în 1826 de către omul de știință francez Jean Poncelet. Dacă în viața de zi cu zi numai munca umană este munca în fizică și, în special, în mecanica se presupune că activitatea se face prin forță. P. cantitatea de funcționare, de obicei, notate cu litera A $ $.

Forța de muncă - este o măsură a forței, în funcție de modul și direcția sa, precum și deplasarea punctului de aplicare a forței. Pentru forța constantă și mișcarea rectilinie a lucrării este determinată de ecuația:

în cazul în care $ F $ - forță care acționează asupra corpului, $ Δr↖ $ - în mișcare, $ $ α - unghiul dintre forța și deplasarea.

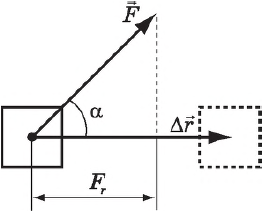
Forța de muncă egală cu produsul forței și modulelor de deplasare și cosinusul unghiului dintre ele, adică. e. produsul scalar al vectorilor $ F↖ $ și $ Δr↖ $.

Ocuparea forței de muncă - cantitatea scalară. Dacă $ $ α 0, iar în cazul în care $ 90 °