Locul geometric al punctelor - studopediya
Definiția.
Locus de puncte (în continuare HMT), numit planul figurii, constând din puncte care au o anumită proprietate, și care nu conțin nici un punct care nu are această proprietate.
Vom lua în considerare numai acele GMT, care pot fi construite cu rigla și compasul.
Luați în considerare locusul pe planul cu cele mai simple și mai frecvent exprimă proprietatea:
1) locus, distanțate la o anumită distanță r de la acest punct O este un cerc cu centrul în punctul de rază r.
2) locul echidistant față de cele două puncte de date A și B este o linie perpendiculară pe segmentul AB și care trece prin mijlocul acesteia.
3) locus echidistant față de cele două linii de date care se intersectează au o pereche de linii perpendiculare reciproc care trec prin punctul de intersecție și care separă unghiurile dintre jumătatea dreaptă.
4) locus, distanțate la distanțe egale h de linie, există două linii drepte paralele cu linia dreaptă și situate pe fiecare parte a ei la această distanță h.
5) Locusul centrelor cercurilor aferente liniei m în M pe acesta punct, este perpendicular pe AB la punctul M (exceptând punctul M).
6) Locusul centrelor cercurilor legate de cerc în această pe acesta ochke M, este o linie dreaptă care trece prin punctul M și centrul cercului (cu excepția punctelor M și O).
7) locus din care segmentul activ este vizibil la un anumit unghi, a două arce de cerc descrise în acest interval și care închide un unghi dat.
8) locus, distanța de la care la punctele două date A și B sunt în raportul m. n, este un cerc (numit Apollonius cerc).
9) Locusul punctele mediane ale corzilor trase dintr-un punct al cercului este cercul construit pe segmentul care unește acest punct la centrul cercului, ca diametru.
10) Locusul vârfurilor triunghiurilor egală cu aceasta și cu o bază comună, două linii drepte este paralelă cu solul și care trece prin vârful triunghiului și este simetric în raport cu linia care conține baza.
Iată câteva exemple de a găsi locusului.
EXEMPLU 2.Find HMT fiind de coarde trase de mijloc dintr-un punct al circumferinței (locus № 9).
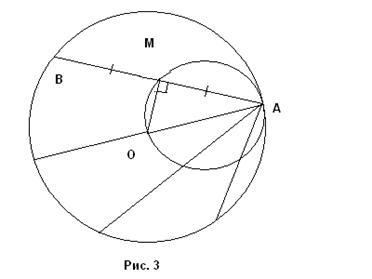
Decizie. Având în vedere un cerc cu centrul O și cercul este ales din punctul A, care sunt deținute coardă. Vom arăta că locul dorit este un cerc construit pe AB ca diametru (cu excepția de la punctul A) (fig. 3).
Să AB - o anumită coardă și M - mijlocul ei. Conectați M și O. Apoi IO ^ AB (rază, coardă împarte în jumătate, perpendicular pe această coardă). dar apoi ÐAMO 90 = 0. De aceea M aparține cu diametrul cercului AB (HMT № 7). pentru că acest cerc trece prin punctul O, atunci G aparține locus nostru.
Pe de altă parte, să presupunem că M aparține locus nostru. Apoi, după ce a petrecut prin coardă M AB și conectarea M și O, constatăm că ÐAMO = 0. 90 adică MO ^ AB, ceea ce înseamnă că M - mijlocul corzii AB. Dacă M coincide cu G, O - mijloc de curent alternativ.
Metoda de coordonate de multe ori vă permite să găsiți locusul.
EXEMPLU 3.Nayti HMT, distanța de la care la două puncte de date A și B sunt, în acest sens m. n (m ≠ n).
Decizie. Alegem un sistem de coordonate dreptunghiular, astfel încât punctele A și B situate pe axa x simetric în jurul originii, iar axa y trece prin centrul AB (Figura 4). Să AB = 2a. Apoi, punctul A are coordonatele A (a, 0), punctul B - Coordonatele (-a, 0). Să presupunem că C aparține locus nostru, coordonatele C (x, y) și CB / CA = m / n. dar mijloacele
Ne transformăm egalitatea noastră. avem
După console de expansiune și reducând termeni similari, obținem
Împărțiți partea stângă și dreaptă a acestei inegalitate a (acest lucru poate fi realizat, deoarece prin ipoteză), apoi selectați un pătrat perfect în ceea ce privește x. obține
Dar ultima ecuație definește un cerc cu centrul și raza Astfel, în cazul în care punctul îndeplinește condițiile problemei, atunci aparține (**).
Invers, să presupunem că coordonatele punctului (x, y) satisfac ecuația (**). Făcând toate calculele în direcția opusă, ajunge la ecuația (*), ceea ce dovedește că locus nostru a punctului.