miresei teoremă, matematică, soluție on-line!

Cred că foarte puțini oameni știau despre unele teorii vor fi discutate, judecând numai din titlul articolului. Astăzi hai sa vorbim despre una dintre teoremele fundamentale ale geometriei - „teorema lui Pitagora“. Este cunoscut de aproape toată lumea, și nu numai pentru aplicarea sa, dar, de asemenea, o mulțime de diferite povești legate de acesta, în numele Creatorului lor înțelept, precum și o mulțime de dovezi. Mai jos sunt listate toate interesante faptele pe care le-am învățat.

Cu siguranță cu toții formularea sa, dar doar în cazul, să-l aducă din nou:
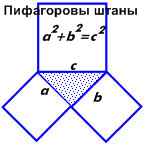
„Într-un triunghi-dreapta, pătratul ipotenuzei este egal cu suma pătratelor celorlalte două părți.“

Pentru a începe să spună de ce este numit „teorema miresei.“ Faptul este că în „elemente“ ale lui Euclid este încă denumit „nimfele teorema.“ ea pur și simplu desen foarte similar cu pcholku sau fluture, iar grecii au fost numite nimfe. Dar când arabii tradus această teoremă, gândul că nimfa - o mireasă. Și așa a ieșit „teorema mireasă“. În plus, în India, este numit „regula de frânghie.“ Acest lucru este valabil cu faptul că, atunci când a fost construit ceva, pentru construirea de Kuta directe au folosit o frânghie, care este rupt în trei părți. De exemplu, luând 12 m și legat cu un capăt de o bară colorată la 3 m, iar cealaltă după 4 m, adică 3 și 4 metri - acesta va fi picioarele (partea directă kuta) și 5 m - ipotenuza. Un „pod de măgari“, numit această teoremă în Germania și Franța.

Există o mulțime de formulare comică a acestei teoreme:
* * *
pantaloni pitagoreice
Pe toate laturile sunt egale.
* * *
În cazul în care un triunghi este dat nouă
Și în plus, cu un unghi drept,
Pătratul ipotenuzei
Noi întotdeauna ușor de găsit:
Picioarele intr-o erectie pătrat,
Am găsit o sumă de puteri
Și, într-un mod simplu
Prin urmare am venit.
* * *

Așa că vreau să rețineți că această teoremă cu cele mai multe dovezi, potrivit Wikipedia, ea le are deja 367. și se bazează pe formularea sa dovedit a fi teoreme suplimentare. Și, deși ei spun că despre o astfel de proprietate triunghi dreptunghic ghicit, chiar cu mult înainte de Pitagora.

Împărtășește cu prietenii:

Evaluați acest articol: