Pregătirea elevilor pentru examenul la rezoluția centru de formare (manual de matematică - elementele

• Obiectivele de interes
• trinom pătratic
• Ecuații și Inegalitățile
  cu module
• Aritmetice și geometrice progresii
• metoda de coordonate
  în avion
• Cifrele pe un plan de coordonate definit de inegalitățile
• Soluție de ecuații algebrice
• Soluția inegalităților raționale
• Decizia de inegalitățile iraționale
• Soluție de ecuații exponențială
• demonstrație Soluție inegalităților
• Soluție ecuații logaritmice
• Soluție inegalitățile logaritmice
• sistemul de ecuații
• Soluție de ecuații trigonometrice
• Trigonometrie în examen
  în matematică
• Gradul cu exponent rațional

MATERIALE INSTRUCȚIONAL OFICIALE

Tangenta la graficul funcției

Desenați secantă graficului y = f (x), care trece prin punctele A și B a graficului, și ia în considerare un caz în care punctul A este fix și punctul B se apropie unlimitedly punctul A de pe graficul funcției y = f (x) (Fig. 2 ).

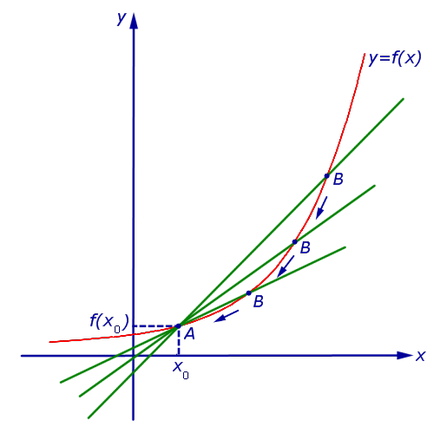
Nelimitat punct de aproximare A la punctul B este desemnat

și să spunem «B se apropie A».

Definiție 2. Dacă x1 → x0 există o poziție limită a grilei de tăiere fuknktsiiy = f (x), atunci aceasta este poziția de limitare a secantă se numește tangenta la graficul y = f (x) la punctul A = (x0; f (x0)) (Figura . 3).

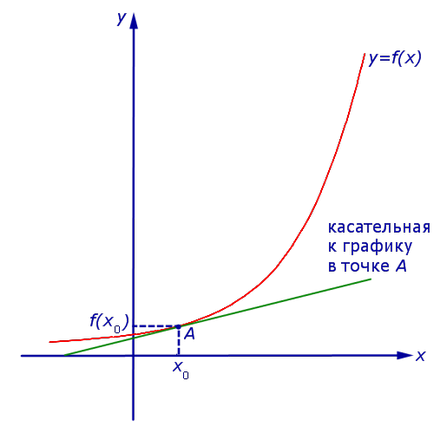
derivat

DEFINIȚIE 3. Dacă raportul x1 → x0

inclusă în formula (4), tinde spre un anumit număr, acest număr se numește derivata funcției y = f (x) la x0. reprezintă f „(x0) și sau înregistrat după cum urmează: