trinom pătrat

Așa că am sunat un polinom. definit prin formula $ a ^> + bx + c $ $ (a \ ne 0) numere $ $ a, b și $ c $ - coeficienții polinomului pătratic, ele sunt de obicei numite :. a - b Senior, - al doilea sau coeficientul mediu c - termenul liber. Funcția de forma y = ax 2 + bx + c se numește o funcție pătratică.

După o funcție liniară a unei funcții pătratice - funcția elementară simplă și importantă. Multe dependență fizică poate fi exprimată printr-o funcție pătratică; de exemplu, o piatră aruncată în sus din v0 de viteză. Se află în momentul t în regiune

de la suprafața pământului (aici, g - accelerația gravitațională); cantitatea de căldură Q, eliberată în timpul trecerii curentului în rezistența conductorului R, exprimat în termeni de formula amperajului I Q = RI 2.

trinom Square. Fig. 1.

trinom Square. Fig. 2.

trinom Square. Fig. 3.

trinom Square. Fig. 4.

Doar un caz special al unei funcții pătratice este o funcție y = ax 2. Fig. 1 prezintă graficele y = ax 2 pentru diferite valori ale. Graful y = ax 2 este numit parabolei.

Toate aceste parabole vârf se află la originea; pentru a> 0 este cel mai jos punct al graficului (cea mai mică valoare a funcției), în timp ce un <0, наоборот, наивысшая точка (наибольшее значение функции). Ось Oy есть ось симметрии каждой из таких парабол.

După cum se poate observa, cu un parabolică> 0 îndreptat în sus, la un <0 — вниз.

Există o modalitate simplă și grafică ușor de utilizat pentru a construi orice număr de puncte ale parabolei y = ax 2 fără calcul, dacă știm punctul de parabole diferit din partea de sus. Lăsați punctul M (x0. Y0) se află pe parabolei y = ax 2 (Fig. 2). Dacă dorim să construim între punctele M și O și mai mult n puncte, apoi se împarte segmentul ON abscisa în n + 1 părți egale și punctele care separă perpendicular pe axa Ox. În aceleași părți egale și se împarte NM puncte de diviziune segment conecta grinzi cu originea. Punctul dorit al parabolei se află la intersecția dintre perpendicularele și grinzi cu aceleași numere (în Fig. 2 Numărul de divizare este de 9 puncte).

Graful y = ax 2 + bx + c este diferit de graficul y = ax 2 numai poziția lor și pot fi obținute prin simpla mișcare a curbei din fig. Din reprezentarea sub forma unui polinom pătratic

de la ușor la concluzia că graficul y = ax 2 + bx + c este un parabole y = ax 2. vârful care sa mutat la punctul

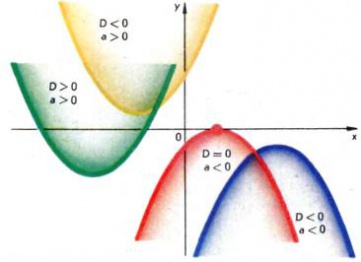
iar axa sa de simetrie rămâne paralelă cu axa Oy (fig. 3). Din această expresie pentru polinomul pătratică este ușor de urmărit toate proprietățile sale de bază. Expresia D = b 2 - 4ac numit discriminantă pătratică ax polinomul 2 + bx + c, iar discriminant asociat toporului ecuației pătratice 2 + bx + c = 0. Din semnul discriminantului depinde dacă graficul traversează axa x polinomul pătratică sau se află pe o parte de la ea. Asta este, dacă D <0, то парабола не имеет общих точек с осью Ox, при этом: если a> 0, atunci parabolei se află deasupra axei Ox, și dacă <0, то ниже этой оси (рис. 4). В случае D> 0 grafic polinom pătratic intersectează axa x la două puncte x1 și x2. care sunt rădăcinile ax ecuației pătratice 2 + bx + c = 0 sunt, respectiv, și

Când D = 0 Ca și pentru axa parabolei în punctul Ox

Proprietățile minciună polinomului pătratic în baza soluției inegalităților pătratic. Să ne explicăm acest lucru cu un exemplu. Să presupunem că doriți să găsiți toate soluțiile inegalității 3x 2 - 2x - 1 <0. Найдем дискриминант квадратного трехчлена, стоящего в левой части неравенства: D = 16. Так как D> 0, atunci ecuația pătratică corespunzătoare 3x 2 - 2x - 1 = 0 are două rădăcini distincte, acestea sunt determinate de ecuațiile prezentate anterior:

In acest trinom pătrat a = 3> 0, atunci se ramifică graf direct valori negative în sus și pătratice polinomială numai în intervalul dintre rădăcini. Deci, toate soluțiile satisfac inegalitățile

La pătrat inegalitățile se poate reduce o varietate de inegalitate prin aceleași substituții care diferite ecuații sunt reduse la pătrat.