Valorile maxime și minime ale funcțiilor în intervalul
Buna ziua tuturor cititorilor mei dragi!
În acest articol vom încerca să învețe cum să se determine valorile maxime și minime ale diferitelor funcții ale punctelor extremum simple și mai complexe, găsirea, pentru a determina dacă minimă extremă valoare sau funcțiile maxime, și chiar distinge funcția de inflexiune a extreme.
vom acționa după cum urmează:
1. Definiți derivata funcției.
2. Asimilarea derivatul la zero pentru a determina dacă extremele funcției are (dacă ecuația rezultată are rădăcini). Va determina dacă datele aparțin extreme ale intervalului specificat.
3. Dacă funcția are un extremum la un interval predeterminat, determina dacă este mare sau mică.
4. Dacă funcția nu are extremum (rădăcini de ecuații obținute prin echivalarea derivatului la zero), determina semnul derivatului. Acest lucru ne va arăta dacă este sau nu funcția de creștere sau descreștere. Apoi vom continua cu condiția problemei: în cazul în care crește funcția, valoarea maximă a părții drepte, iar cea minimă - la stânga. În cazul în care scăderea - dimpotrivă. rezolvarea problemelor ne va ajuta toate pentru a sorta prin intermediul și cu ajutorul imaginilor, vom încerca să nu părăsească locurile obscure în rezolvarea unor astfel de probleme.
Problema 1. Este necesar să se determine cea mai mare valoare a funcției:

Ne desfasuram activitatea conform algoritmului, mai întâi determină derivata. Aici avem suma funcțiilor, astfel încât definim derivata fiecare separat și se adaugă în sus, iar apoi echivala derivatul cu zero:
Rezolvăm ecuația rezultată. Dacă rădăcinile sunt - atunci, probabil, avem extreme (punctul în care derivatul este zero, nu poate fi un extremum, iar punctul de inflexiune).

Vedem - rădăcină este:

În acest moment, funcția noastră are o extremă. Este important ca acest punct aparține unui anumit interval. Aflați mai minimum.Dlya acest lucru sau de care are nevoie pentru a determina semnul instrumentului derivat în vecinătatea acestui punct, adică, dreapta și stânga din ea. De exemplu, puteți lua punctul - acesta este pe partea stângă, iar punctul - va fi corect. apoi:

Este clar că funcția are o valoare maximă la punctul maksimuma.Naydem această valoare, după cum urmează: Substituind punctul funcției extremum în ecuația:
A: Cea mai mare valoare a funcției, la un anumit interval de timp este de 10.
2.Find cea mai mică valoare a funcției la un anumit interval:
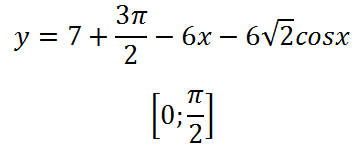
În același mod ca și pentru prima dată, vom lua derivatul și egală cu zero:
Deja este clar că această ecuație are rădăcinile:

La punctul funcția are o extremă. Maximă sau minimă este? Să ne găsim valoarea derivatului pe dreapta și la stânga punctului. Din nou, vom lua un punct - acesta va fi situat pe partea stângă, iar punctul - va fi corect. apoi:


Funcția ia cea mai mică valoare de la punctul m inimuma, l-am găsit:
Răspuns: Valoarea minimă a funcției în acest interval este de 1.
Să ne rezolve următoarea problemă:
3. Se determină cea mai mare valoare a intervalului:

În primul rând, ca întotdeauna, derivatul:

Acesta este cazul când extremele funcției în acest interval este: în ecuația de mai sus nu are rădăcini. Acest lucru înseamnă că funcția este monotonă, fie scade sau crește. Putem determina acest lucru prin semnul derivat în cazul în care derivatul este pozitiv - crește funcția, dacă este negativ - în scădere. De ce avem nevoie să știm crește sau scade funcția? Faptul este că, în cazul în care funcția crește, valoarea sa va fi întotdeauna mai mare la capătul din dreapta al intervalului, și scade în cazul în care - în partea stângă.

În țara noastră, indiferent de ce unghi vom lua, pentru că acesta este mai mic de 1, astfel încât derivatul este pozitiv, ceea ce înseamnă că funcția este în creștere. Astfel, valoarea sa maximă ajunge la punctul 0:
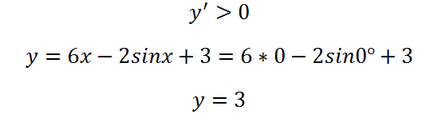
4. Se determină valoarea minimă a funcției pe segmentul:

Definim derivatul și echivala cu zero:
Deja este clar că funcția este monotonă (rădăcini ale ecuației rezultată):

Deoarece derivatul este negativ, atunci vom trage concluzia că funcția scade. Apoi, cea mai mică valoare - la capătul din dreapta al segmentului, și anume 0:
Răspuns: Valoarea minimă a funcției pe un anumit interval de - 19.
5. Găsiți cea mai mică valoare a funcției pe segmentul:

Ia echivaleaza derivatul cu zero și rezolvarea ecuației rezultă:
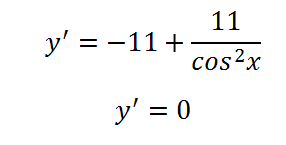

S-ar părea - ecuația are rădăcini, astfel încât funcția va avea o valoare extremă în acest segment (a doua rădăcină a acestui segment nu face parte, astfel încât să nu fie luate în considerare). Definiți o valoare maximă sau minimă este. O valoare de 1 pentru cosinusul - maxim, adică, un moment dat sau de a lua o aproape de zero - cosinusul - abscisa - va fi mai mică decât la zero. Cu toate acestea! Derivata punctul de reper zero, nu se schimba! Este pozitiv în vecinătatea zero, iar apoi crește în funcție de zero, și după. Deci, funcția de la punctul de zero, nu are nici o extremelor și inflexiune.

Prin urmare, pentru a determina cea mai mică valoare, trebuie să ia capătul din stânga al segmentului și numără valoarea funcției în acel moment. Printr-o coincidenta fericita, acest punct de zero. Cu toate acestea, ar putea fi un alt punct diferit de zero, iar apoi am putea face o greșeală, având în vedere punctul de extremelor la zero, și determinarea valorii unei funcții în ea. Astfel, valoarea funcției:
Răspuns: Valoarea minimă a funcției pe un anumit interval de - 8.
6. Găsiți punctul funcției maxime:
Algoritmul executarea acestor sarcini sunt aceleași. Mai întâi de toate - instrumentul derivat. Aici avem produsul a două funcții, astfel încât să luăm derivata statului de a lua derivat din caracteristicile produsului:
echivala în continuare această expresie la zero. Este clar că exponentul este întotdeauna non-negativ, într-un anumit grad sau ridicat, astfel încât rădăcina „ascuns“ în al doilea factor:

Asigurați-vă că acest extremelor - maxim. Într-adevăr, în acest moment Derivatul modificările semn, și modificările de la pozitiv la negativ, adică, până la acest punct crește funcției, și după - scăderi.
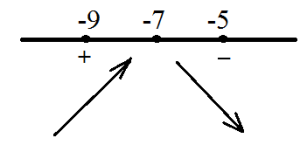
7. Găsiți cea mai mică valoare a funcției pe segmentul:
Vom, ca de obicei, pentru a găsi derivata acestei funcții, iar această funcție este complex: (! Si un grad - chiar dacă face sa semneze jurnalul, este necesar să se pună modulul de conectare, astfel încât să nu pentru a restrânge definiția funcției) logaritmului exprimată în grade. Prin urmare, pentru a nu dezvălui modul, putem folosi regula de a lua derivata unei funcții compozit:
Expresia rezultată este egală cu zero:

Rețineți că punctul (3) derivatul nu este definit. Cu toate acestea, în acest moment modificările derivate semneze. Litera (-2) - funcția minimă, deoarece schimbările derivate semn de la negativ la pozitiv. Prin urmare, în acest moment valoarea minimă funcției. Găsiți-l:
Răspuns: Valoarea minimă a funcției pe un anumit interval de - 8.
8. Localizați punctul funcției maxime:
Noi determinăm derivata unei funcții compozit. S-au găsit echivala derivatul cu zero:

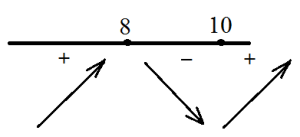
Avem două puncte de extreme. Unul dintre ei - maxim, celălalt - cel puțin.
Funcția are un maxim la 8.
9. Găsiți punctul de minim al funcției:
Se determină lucrări derivate, în plus, exponentul este o funcție complexă (aici, derivatul de măsura în care a ridicat exponent 1 este egal). S-au găsit echivala derivatul cu zero:

Punctul minim al funcției este punctul 11. Acest lucru poate fi văzut: derivatul în ea schimbă semn de la minus la plus.
Raspuns: x = 11.
10. Găsiți punctul minim și maxim al funcției:
Noi determinăm derivata unei funcții compozit. S-au găsit echivala derivatul cu zero:

Derivata acestei funcții schimbă semn de la negativ la pozitiv la punctul 2 (minim) și de la pozitiv la negativ - la 17 (maxim).
11. Găsiți cea mai mică valoare a funcției pe segmentul:
Menționăm că expresia sub logaritmul este mai mare decât zero. 0 "title =" x + 3> 0 "/> [/ pmath] -3" title = "x> -3" /> [/ pmath]. Segmentul pe care o vom examina și de a determina funcția semnelor derivate satisface domeniul funcției.
Să ne găsim derivatul și echivala cu zero:

La punctul 2, modificările derivate semn, atunci este extrem. Se schimbă semn de la negativ la pozitiv, astfel încât acest punct - punctul de minim. Este nevoie de cea mai mică valoare a funcției:
Răspuns: Valoarea minimă a funcției pe un anumit interval de - 8.
12. Găsiți cea mai mică valoare a funcției pe segmentul:

Să ne găsim derivatul și echivala cu zero:
Poate fi remarcat faptul că domeniul funcției - valori pozitive ale lui x (ca expresie a logaritmului mai mare decât zero), și că derivatul de la punctul 0 nu este ecuația de gradul doi opredelena.Poluchim în care suma coeficienților egal cu 0 (a + b + c = 0) . În această ecuație, o rădăcină este 1 și a doua c / a:

Adresați-vă un segment aparține doar un singur punct - 1. Derivatul aici Modificări semn de la negativ la pozitiv, și, prin urmare, acesta este un minim. Definim valoarea funcției în acest moment:
13. Găsiți cea mai mică valoare a funcției pe segmentul:

Rețineți că funcția nu este definită la punctul 0.
Noi luăm derivatul fracției:

Egalăm derivatul la zero, iar noi căutăm rădăcinile:

Una dintre rădăcinile nu ne interesează, pentru că diferența nu aparține, iar al doilea punct al modificărilor derivate semn de la negativ la polozhitelnyy.To o funcție are un minim în acest moment. Definiți valoarea minimă:
