coliziuni elastice și inelastice

1.21. coliziuni elastice și inelastice

Legea conservării energiei mecanice și legea conservării impulsului de a găsi soluții pentru a permite probleme mecanice în cazurile în care forțele care acționează sunt necunoscute. Un exemplu de astfel de probleme este impactul interacțiunii corpurilor.

Interacțiunea cu organismele de șoc au de multe ori să se ocupe în viața de zi cu zi în domeniu și în fizică (în special în fizică și un atom de particule elementare).

Stroke (sau coliziune) se numește interacțiune tranzitorie a organelor, ca urmare a care viteza lor prin schimbări semnificative. La momentul impactului dintre ele sunt forțe de șoc scurte, valoarea care este de obicei necunoscuta. Prin urmare, ciocanul nu poate fi văzut în mod direct prin interacțiunea dintre legile lui Newton. Aplicarea legilor de conservare a energiei și de impuls, în multe cazuri, pentru a elimina din luarea în considerare a procesului de coliziune în sine și pentru a obține relația dintre vitezele de corpuri, înainte și după coliziune, ocolind toate valorile intermediare ale acestor cantități.

Mecanicii sunt adesea folosite două modele de interacțiune șoc - coliziune complet elastică și complet neelastic.

Complet ciocan de impact inelastic se numește interacțiune, în care corpul alăturat (Coalesce), unul cu altul și pentru a muta pe un singur corp.

Atunci când coliziune complet inelastică energie mecanică nu este conservată. Acesta este convertit parțial sau complet în energie internă a corpurilor (încălzire).

Un exemplu de impact complet inelastic poate servi gloanțe lovit (sau coajă) într-un pendul balistic. Pendulul este o cutie cu nisip de masă M. suspendat pe corzi (Fig. 1.21.1). Bullet masa m. zboară orizontal la rateaza cutia si blocat acolo. La deformarea pendulului poate determina viteza unui glonț.

Notăm cutie de viteză cu un glonț în ea blocată prin timp potrivit legii conservării impulsului

Dulcețuri gloanțe în nisip a fost o pierdere de energie mecanică:

Raportul M / (M + m) - proporția energiei cinetice a glonțului care a trecut în energia internă a sistemului:

Această formulă este aplicabilă nu numai la pendulul balistice, dar, de asemenea, la orice coliziune inelastică a două corpuri cu diferite mase.

pentru m <> M) raportul

deplasarea în continuare a pendulului poate fi calculată folosind legea de conservare a energiei mecanice:

în cazul în care h - înălțimea maximă de ridicare pendul. Din aceste relații rezultă:

Prin măsurarea înălțimii h pe experiența ascensorului pendul, puteți determina viteza glonțului v.

Perfect coliziune elastică se numește o coliziune în care energia mecanică este stocată sistem telefonic.

In multe cazuri, ciocnirea atomilor, molecule și particule elementare se supun legilor coliziune perfect elastică.

Atunci când coliziune complet elastică, împreună cu legea de conservare a impulsului legea de conservare a energiei mecanice.

Un exemplu simplu de coliziune perfect elastică poate fi două bile centrale impact de biliard, dintre care unul era în fața stării de coliziune repaus (fig. 1.21.2).

mingi de volei centrale numit coliziune, viteza la care bilele înainte și după impact sunt îndreptate de-a lungul liniei de centre.

Absolut elastic bile centrale împușcat

În general, bilele de masă m 1 și m 2 care se ciocnesc pot fi inegale. Conform legii de conservare a energiei mecanice

Nu υ1 - prima treaptă de viteză înainte de coliziune mingii, viteza a doua minge υ2 0. u = 1 și u 2 - bile viteza după ciocnire. Legea conservării impulsului pentru viteze proiecțiilor pe axa de coordonate îndreptate de-a lungul primei viteza mingii înainte de impact, scrisă sub forma:

Avem un sistem de două ecuații. Acest sistem poate fi rezolvată pentru a găsi viteza necunoscută u 1 și u 2 bile după ciocnire:

În cazul special în care ambele bile au aceeași masă (m 1 = m 2), prima minge după impact se oprește (u 1 = 0), iar a doua se deplasează cu viteza u 2 = υ1. t. e. schimb de bile viteze (și, prin urmare, impuls).

Dacă ciocnirea a doua minge a avut o viteză de zero (υ2 ≠ 0), atunci această problemă poate fi ușor redusă la cea precedentă printr-o tranziție într-un nou cadru de referință, care se mișcă uniform într-o linie dreaptă la o viteză de Y2 în raport cu sistemul „fix“. În acest sistem, a doua minge se sprijină înainte de coliziune, iar prima lege a compoziției vitezei are o viteză υ1 „= υ1 - υ2. După ce a definit prin formulele de mai sus viteza u 1 și u 2 bile după ciocnire în noul sistem, aveți nevoie pentru a face trecerea înapoi la sistemul „staționar“.

Astfel, folosind legile conservării energiei mecanice și impuls, viteza poate fi determinată după coliziune de bile în cazul în care acestea sunt cunoscute la viteza de coliziune.

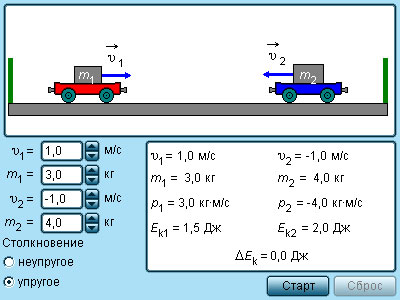
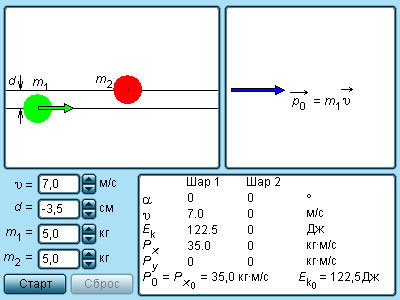
Modelul. coliziuni elastice și inelastice

Central (frontală) a lovit foarte rar pus în practică, mai ales în cazul unor coliziuni de atomi sau molecule. Când viteza de excentrică coliziune elastică a particulelor (sfere), înainte și după ciocnire nu este îndreptată de-a lungul aceleiași linii.

Un caz particular de excentrică coliziune impact elastic poate servi două bile de biliard de greutate egală, la una dintre care coliziune a fost fixată, iar a doua viteză nu urmărește linia centrală a bile (Fig. 1.21.3).

coliziune elastic excentrică bile de aceeași greutate. d - parametrul de impact

După un off-centru de bile coliziune zbura la un anumit unghi unul de altul. Pentru a determina viteza după impact și trebuie să cunoască poziția centrului liniei la momentul impactului sau impact distanța d (Fig. 1.21.3), m. E. Distanța dintre două linii trasate prin centrele bile de minge paralelă cu vectorul vitezei proiectilului. În cazul în care masele de bile sunt aceleași, vectorul viteză și bilele după ciocnire elastică întotdeauna îndreptată perpendicular unul pe altul. Este ușor de a arăta, folosind legile de conservare a impulsului și a energiei. Când m 1 = m 2 = m aceste legi devin:

Primul dintre aceste ecuații indică faptul că vectorii de viteza, și formează un triunghi (diagrama puls), iar al doilea - ca pentru acest triunghi pitagoreic teoremă, adică, este dreptunghiular ... Unghiul dintre picioare și este egală cu 90 °.