Înscrisă în minge piramida
Atunci când sarcina este dată o minge înscrisă în piramida, soluția sa va folosi următoarele informații teoretice.
Dacă piramida se înscrie într-o sferă, atunci toate nodurile sale se află pe suprafața sferei (în sfera), respectiv, distanțele de centru mingea la nodurile egale cu raza mingea.
Fiecare figură înscrisă într-o sferă a piramidei este înscrisă într-un cerc poligon. Bazele perpendicularele a scăzut de la centrul sferei pe fețele plane sunt centrele cercurilor circumscrise. Astfel, centrul sferei circumscris despre piramida - punctul de intersecție perpendicular pe fețele piramidei, trase prin centrele cercurilor din jurul fețelor.
Cele mai multe centre-a descris în jurul mingea piramidei sunt considerate ca fiind punctul de intersecție al perpendicularei trase la baza prin intermediul centrului despre cercul de bază și perpendiculară pe muchia laterală (perpendicular bisector se află într-un plan care trece prin această muchie laterală și o primă perpendiculară (ținut la bază.) Dacă nu se poate descrie un cerc în jurul bazei piramidei, această piramidă nu poate fi înscris într-o sferă. aceasta implică faptul că aproximativ o piramidă triunghiulară este întotdeauna posibil să se descrie mingea, așa cum înscris în mingea ciudat rehugolnaya piramidă în baza unui dreptunghi sau pătrat.
Despre centrul minge piramide descrise se poate afla în interiorul piramidei, piramida pe suprafața (pe fața laterală, pe sol), și este piramidă. În cazul în care declarația problema nu spune exact în cazul în care centrul este descris de lume, este de dorit să se ia în considerare, deoarece acestea pot influența decizia diferitelor opțiuni pentru locația sa.
Despre orice drept al piramidei poate fi descrisă ca o minge. Centrul său - punctul de intersecție al liniei care conține înălțimea piramidei și perpendicular pe marginea laterală.
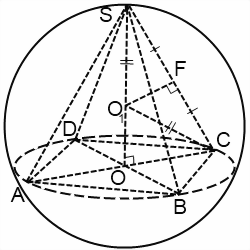
În rezolvarea problemelor pe o minge înscris într-o piramidă adesea considerate unele dintre triunghiuri.
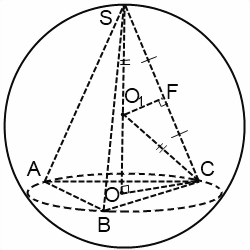
Să începem cu triunghi SO1C. Se isoscel pentru că două dintre laturile sale sunt egale cu razele sferei: OS1 = O1S = R. În consecință, O1F - înălțimea sa, mediana si bisectoare.
Dreptul Triunghiuri SOC și SFO1 ca colțul ascuțit al S. Prin urmare,
SO = H - înălțimea piramidei, SC = b - lungimea marginilor laterale, SF = b / 2, SO1 = R, OC = r - raza unui cerc circumscris baza piramidei.
În triunghiul în unghi drept ipotenuzei OO1C g O1C = R, picioareleor OC = r, OO1 = H-R. Prin teorema lui Pitagora:
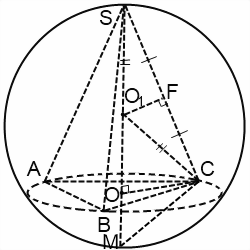
Dacă continuați înălțimea SO, obținem diametrul SM. SCM Triangle - dreptunghiular (din unghiul CSM inscripționată pe baza diametrului). Există OC - înălțimea trase la ipotenuzei, SO și OM - proiecție a picioarelor CS și CM pe ipotenuza. Conform proprietăților unui triunghi dreptunghic,
și încă o dată, doar un alt mod:
Aceste argumente sunt valabile nu numai pentru piramida regulată, dar, de asemenea, pentru piramida. înălțimea de bază, care este centrul de cerc în jurul bazei piramidei.